Conjuntos

Conjuntos, em inglês sets, são uma estrutura de dados interessante (e pouco falada, na minha visão). São coleções mas não são considerados sequências, como listas e tuplas, por não preservarem a ordem e os itens não poderem ser acessados por posição, tendo assim algumas características distintas:

• Elementos únicos: Um conjunto não permite que elementos duplicados sejam armazenados. Se você tentar adicionar o mesmo elemento mais de uma vez, ele será armazenado apenas uma vez.

• Sem ordem definida: Os elementos em um conjunto não têm uma ordem específica. Diferente de listas ou tuplas, onde a ordem dos elementos é importante, em conjuntos a posição dos elementos não é garantida e pode variar.

• Operações matemáticas: Conjuntos suportam operações matemáticas como união, interseção, diferença e diferença simétrica, que são úteis para comparar e combinar conjuntos de dados.

Vamos aprofundar mais neste capítulo. Sugiro fortemente que você leia a documntação oficial sobre conjuntos aqui, ela é a base deste capítulo todo.

Sintaxe básica

a sintaxe básica para criar um conjunto (set) envolve colocar os elementos entre chaves {}. Por exemplo, conjunto = {1, 2, 3, 3} cria um conjunto contendo os números 1, 2 e 3 (o 3 aparece apenas uma vez, pois o conjunto elimina duplicatas de forma automática).

conjunto = {1, 2, 3, 3}
print(conjunto)

{1, 2, 3}

A diferença entre a sintaxe de um conjunto e a de um dicionário está no formato e no propósito de cada estrutura, apesar de ambos se iniciarem com {}.

Nota (type)

Lembra da função type? Se quiser de fato conferir se uma variável que começa e termina com {} é um conjunto ou dicionário, é possível verificar com a função type.

Um conjunto é uma coleção de elementos únicos, sem nenhuma relação de chave e valor, e os elementos são separados por vírgulas dentro das chaves. Já um dicionário também é criado com chaves {}, mas ele armazena pares de chave e valor, como pessoa = {"nome": "João", "idade": 30}. No dicionário, cada chave é associada a um valor específico, enquanto no conjunto, você apenas tem valores sem uma chave correspondente.

Portanto, a principal diferença na sintaxe é que em um conjunto, você apenas lista os elementos, enquanto em um dicionário, você precisa especificar chaves e valores, separados por dois pontos :.

Caso de uso real

Supondo que uma pessoa A tenha uma carteira de investimento com os seguintes fundos imobiliários: BPFF11, BTLG11, CSHG11, FEXC11, FIIB11, HFOF11, HGLG11 e HGRE11.

Uma outra pessoa B também tem uma outra carteira de fundos imobiliários com os seguintes fundos: BCFF11, FIIJ11, GGRC11, HFOF11, HGLG11, HGLG11, HGPO11 e HGRU11.

Com conjuntos podemos rapidamente responder às seguintes perguntas:

investimentos_pessoa_a = {
    "BPFF11",
    "BTLG11",
    "CSHG11",
    "FEXC11",
    "FIIB11",
    "HFOF11",
    "HGLG11",
    "HGRE11",
}
investimentos_pessoa_b = {
    "BCFF11",
    "FIIJ11",
    "GGRC11",
    "HFOF11",
    "HGLG11",
    "HGLG11",
    "HGPO11",
    "HGRU11",
}

# Quais são os ativos em comum entre as pessoas A e B?
investimentos_em_comum = investimentos_pessoa_a.intersection(investimentos_pessoa_b)
print(investimentos_em_comum)

{'HGLG11', 'HFOF11'}

investimentos_pessoa_a = {
    "BPFF11",
    "BTLG11",
    "CSHG11",
    "FEXC11",
    "FIIB11",
    "HFOF11",
    "HGLG11",
    "HGRE11",
}
investimentos_pessoa_b = {
    "BCFF11",
    "FIIJ11",
    "GGRC11",
    "HFOF11",
    "HGLG11",
    "HGLG11",
    "HGPO11",
    "HGRU11",
}

# Quais são os ativos das carteiras de ambas as pessoas (A, B ou ambas)?
todos_os_ativos = investimentos_pessoa_a.union(investimentos_pessoa_b)
print(todos_os_ativos)

{'BPFF11', 'CSHG11', 'FIIB11', 'BCFF11', 'HGRE11', 'HGRU11', 'HFOF11', 'GGRC11', 'HGPO11', 'FEXC11', 'HGLG11', 'BTLG11', 'FIIJ11'}

investimentos_pessoa_a = {
    "BPFF11",
    "BTLG11",
    "CSHG11",
    "FEXC11",
    "FIIB11",
    "HFOF11",
    "HGLG11",
    "HGRE11",
}
investimentos_pessoa_b = {
    "BCFF11",
    "FIIJ11",
    "GGRC11",
    "HFOF11",
    "HGLG11",
    "HGLG11",
    "HGPO11",
    "HGRU11",
}

# Quais são os ativos que somente a pessoa A tem em carteira?
investimentos_exclusivos_pessoa_a = investimentos_pessoa_a - investimentos_pessoa_b
print(investimentos_exclusivos_pessoa_a)

{'BPFF11', 'CSHG11', 'FIIB11', 'HGRE11', 'FEXC11', 'BTLG11'}

investimentos_pessoa_a = {
    "BPFF11",
    "BTLG11",
    "CSHG11",
    "FEXC11",
    "FIIB11",
    "HFOF11",
    "HGLG11",
    "HGRE11",
}
investimentos_pessoa_b = {
    "BCFF11",
    "FIIJ11",
    "GGRC11",
    "HFOF11",
    "HGLG11",
    "HGLG11",
    "HGPO11",
    "HGRU11",
}

# Quais são os ativos que somente a pessoa B tem em carteira?
investimentos_exclusivos_pessoa_b = investimentos_pessoa_b - investimentos_pessoa_a
print(investimentos_exclusivos_pessoa_b)

{'BCFF11', 'HGRU11', 'GGRC11', 'HGPO11', 'FIIJ11'}

Teoria dos conjuntos

Conjuntos são a estrutura ideal para trabalharmos pensando em teoria dos conjuntos. Na teoria dos conjuntos, trabalhamos com operações que nos ajudam a combinar, comparar e manipular coleções de elementos. Em Python, a estrutura de dados conjunto (set) oferece uma maneira eficiente de realizar essas operações. Vamos explorar as principais operações entre conjuntos.

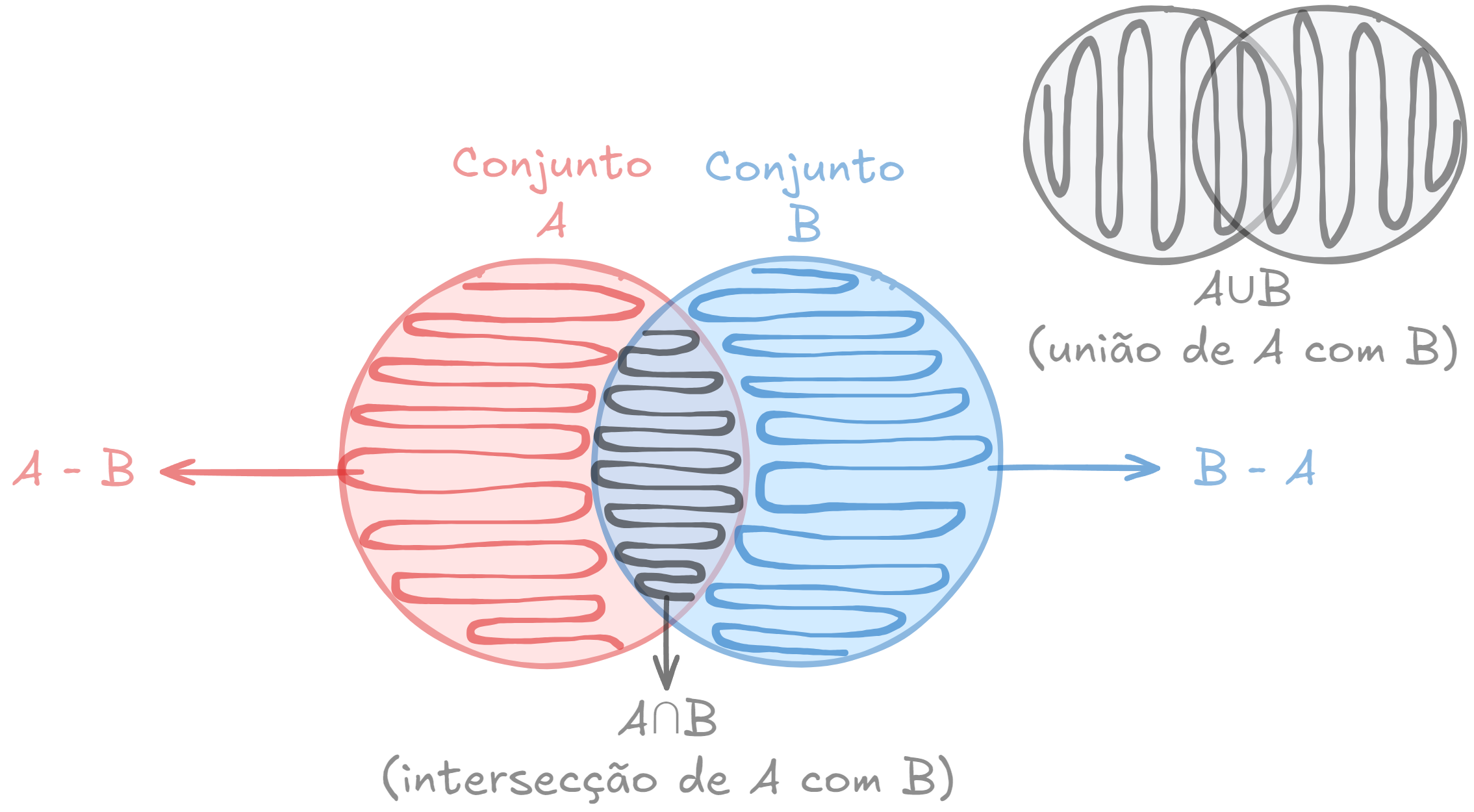
Teoria dos conjuntos (fonte: autoria própria)

União (Union)

A união de dois conjuntos A e B resulta em um novo conjunto que contém todos os elementos de A e B, sem duplicatas. Em Python, usamos o operador | ou o método .union() para realizar a união.

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

# Operador |
uniao = conjunto_a | conjunto_b
print(uniao)

uniao = conjunto_a.union(conjunto_b)

{1, 2, 3, 4, 5}

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

# Método .union()
uniao = conjunto_a.union(conjunto_b)
print(uniao)

{1, 2, 3, 4, 5}

Intersecção (Intersection)

A intersecção de dois conjuntos A e B resulta em um novo conjunto que contém apenas os elementos que estão em ambos os conjuntos. Em Python, usamos o operador & ou o método .intersection().

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

interseccao = conjunto_a & conjunto_b
print(interseccao)

{3}

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

interseccao = conjunto_a.intersection(conjunto_b)
print(interseccao)

{3}

Diferença (Difference)

A diferença entre dois conjuntos A e B resulta em um novo conjunto que contém os elementos que estão em A, mas não em B. Usamos o operador de menos - ou o método .difference().

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

diferenca = conjunto_a - conjunto_b
print(diferenca)

{1, 2}

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

diferenca = conjunto_a.difference(conjunto_b)
print(diferenca)

{1, 2}

Diferença simétrica (symmetric difference)

A diferença simétrica entre dois conjuntos A e B resulta em um novo conjunto que contém os elementos que estão em A ou B, mas não em ambos. Usamos o operador ^ ou o método .symmetric_difference().

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

diferenca_simetrica = conjunto_a.symmetric_difference(conjunto_b)
print(diferenca_simetrica)

{1, 2, 4, 5}

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

diferenca_simetrica = conjunto_a ^ conjunto_b
print(diferenca_simetrica)

{1, 2, 4, 5}

Verificação de continência (subconjunto e superconjunto)

• Subconjunto (subset): Verifica se todos os elementos de um conjunto estão presentes em outro conjunto. Usamos o operador <= ou o método .issubset().

• Superconjunto (superset): Verifica se todos os elementos de um conjunto estão presentes em outro conjunto. Usamos o operador >= ou o método .issuperset().

conjunto_a = {1, 2, 3}
conjunto_b = {3, 4, 5}

conjunto_c = {1, 2}

print("Subconjunto")
print(
    f"O conjunto C é um subconjunto de A? Usando o operador <= : {conjunto_c <= conjunto_a}"
)
print(
    f"O conjunto C é um subconjunto de A? Usando o método .issubset() : {conjunto_c.issubset(conjunto_a)}\n"
)

print("Superconjunto")
print(
    f"O conjunto B é um superconjunto de C? Usando o operador >= : {conjunto_b >= conjunto_c}"
)
print(
    f"O conjunto B é um superconjunto de C? Usando o método .issuperset() : {conjunto_b.issuperset(conjunto_c)}"
)

Subconjunto
O conjunto C é um subconjunto de A? Usando o operador <= : True
O conjunto C é um subconjunto de A? Usando o método .issubset() : True

Superconjunto
O conjunto B é um superconjunto de C? Usando o operador >= : False
O conjunto B é um superconjunto de C? Usando o método .issuperset() : False

Pertencimento

Podemos verificar se um elemento pertence a um conjunto usando o operador in ou not in.

conjunto_a = {1, 2, 3}

# Pertence
print(2 in conjunto_a)

# Não pertence
print(6 not in conjunto_a)

True
True

Prática

Sugiro o exercício 11 da lista para você praticar a estrutura de conjuntos.

Conclusão

Neste capítulo, exploramos em detalhes os conjuntos em Python, uma estrutura de dados fundamental para lidar com teoria dos conjuntos. Aprendemos que conjuntos são coleções não ordenadas de elementos únicos, o que os torna extremamente úteis para tarefas como remoção de duplicatas, testes de pertinência e operações entre conjuntos.

Vimos como criar conjuntos, adicionar e remover elementos, e realizar operações comuns, como união, interseção e diferença. Exploramos as principais propriedades dos conjuntos, como a impossibilidade de duplicatas e a natureza desordenada dos elementos. Isso os torna uma escolha ideal quando a ordem dos elementos não é relevante, mas a unicidade é essencial.

Além disso, discutimos o uso prático de conjuntos em situações do mundo real, como verificação de ações exclusivas em carteiras de investimentos, identificação de amigos em comum em redes sociais e muito mais. Demonstramos como os conjuntos podem simplificar significativamente muitos problemas comuns, tornando-os uma ferramenta essencial no arsenal do desenvolvedor Python.

À medida que você continuar a explorar a linguagem Python, recomendo manter os conjuntos em mente e considerar seu uso sempre que precisar trabalhar com coleções de elementos únicos. Sua eficiência e sua sintaxe concisa os tornam uma opção poderosa para uma ampla gama de tarefas de programação.

Com o domínio das estruturas de dados básicas, como strings, listas, tuplas, dicionários e conjuntos, agora estamos prontos para avançar para o próximo tópico: fluxos de controle. Lá, aprenderemos a criar estruturas de decisão, os famosos if-else-elif e de repetição, for e while, que nos permitirão escrever códigos cada vez mais sofisticados e adaptáveis.